Extension 6.4: Fibonacci Recursively and Iteratively¶

Authors¶

Background¶

The Fibonacci Sequence is an interesting pattern of numbers that occurs in a lot of unusual places. The first number in the sequence is 0, the second number is 1, the third is also 1, the fourth is 2, the fifth is 3, the sixth is 5, ….

Each new number in this sequence is just the sum of the previous two numbers. This can be expressed via a recursive equation, like:

\[\begin{split}fib(n) = \begin{cases} 0, & \text{if}\ n=0 \\ 1, & \text{if}\ n=1, \\ fib(n-1)+ fib(n-2), & \text{otherwise} \end{cases}\end{split}\]

Since this formula is recursive, it can easily be represented in recursive computer code.

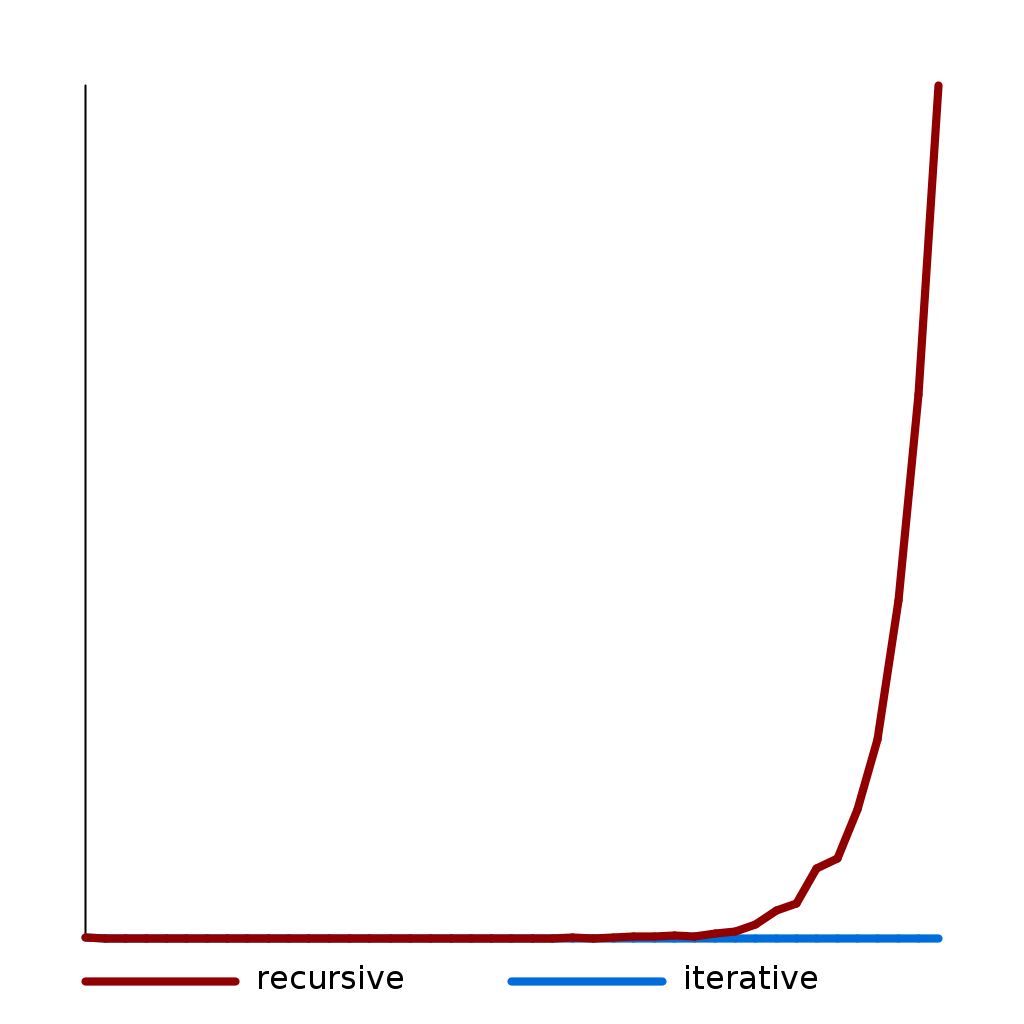
In this extension, you will compare the running time of that recursive formulation with an iterative formulation of the same function.

Why Fibonacci?¶

Procedure¶

You should see a fibonacci package in the nonexam folder. You will modify Graph.java and Fibonacci.java. They are both already in the respository.

Graph¶

Complete graphLine(ys) in Graph.

Note: You should assume that StdDraw’s x and y scales are configured to allow the index of the array to map to the x-coordinate and the value at that index to be the y-coordinate.

Run Graph as a Java Application.

Fibonacci¶

You will complete two methods in the Fibonacci class: recursive(n) and iterative(n). You will complete graphLine(ys) in the Graph class.
Complete the recursive method in Fibonacci so that it returns the n ^th fibonacci number using recursion. (You can base it on the recursive equation provided above.)
Run FibonacciTestSuite until you have passed all of the recursive portion.
Complete the iterative method in Fibonacci so that it computes the same function, but iteratively.
As a hint, you will need two variables that represent the (n-1) :sup:th and (n-2) ^th values of the sequence. Adding those together produces the n :sup:`th`term. The variables’ values are then shifted prior to the next iteration.
Run FibonacciTestSuite until you have passed all of the tests.

Testing¶

To run the suite of unit tests, right (control) click on FibonacciTestSuite and choose Run as... then JUnit Test.

Timing¶

Run FibonacciDebugApp to get timing information on your algorithms.

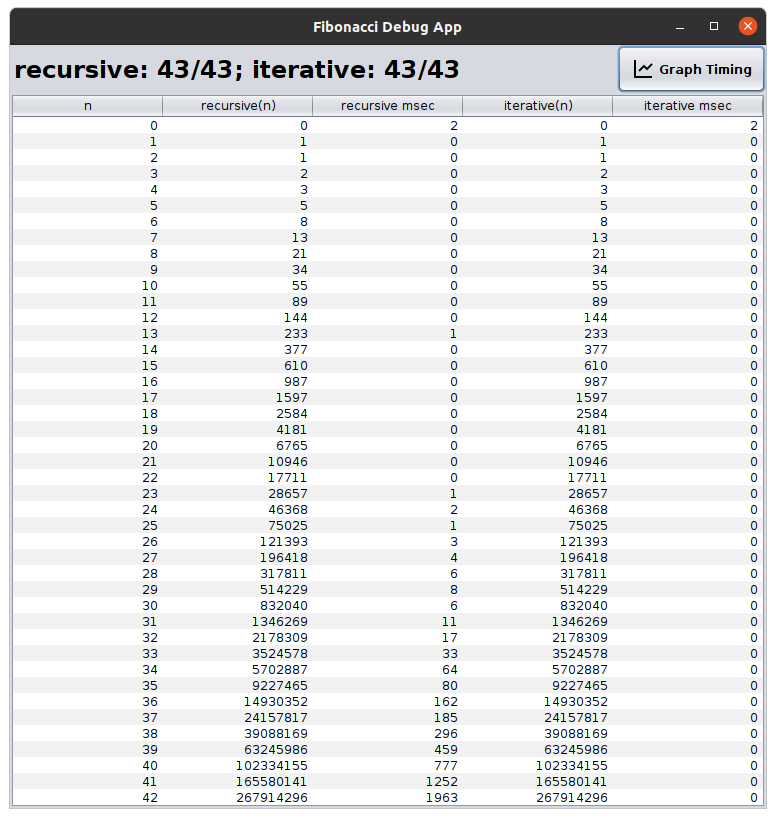
Press the Graph Timing button to see your graphLine(ys) method draw the timing data.

You have attempted of activities on this page