Extension 5.6: Star Sines¶
Background¶
In this extension we will use StdDraw to create a method that draws stars with any given odd number of points at any given rotation angle.
Polar Coordinates¶
It may be useful to think about how you convert from polar coordinates (rho, theta) to cartesian coordinates (x, y) to aid you in how you tackle this problem.
Filled Polygon¶
For a demo on how to use StdDraw.filledPolygon(xs, ys) check out this video:
Code from the video:
double[] xs = {0.1, 0.9, 0.5, 0.3, 0.6};
double[] ys = {0.1, 0.1, 0.5, 0.2, 0.05};
StdDraw.filledPolygon(xs, ys);
Image produced from code above:

Procedure¶
A clean, elegant solution is desirable and achievable to this extension. You should require only Math.cos(radians), Math.sin(radians), StdDraw.filledPolygon(xs, ys), and a single loop.
Note: Credit will only be awarded for clean, elegant solutions.
Recall From High School Trigonometry: you can get the x-coordinate of a point on the unit (radius 1) circle at an angle theta with Math.cos(thetaInRadians). You can get the y-coordinate with Math.sin(thetaInRadians).
Plan¶
Perhaps you recall drawing a five pointed star as a child:
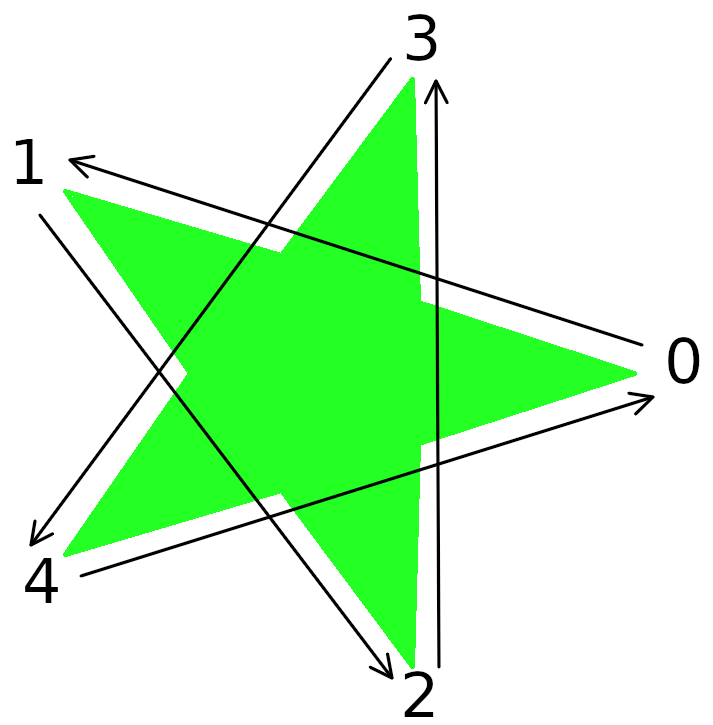
Note: There is nothing wrong with the drawing-10-points-for-a-5-pointed-star technique. This technique will also work. However, it is likely that the 5-points-for-a-5-pointed-star technique is cleaner and easier.
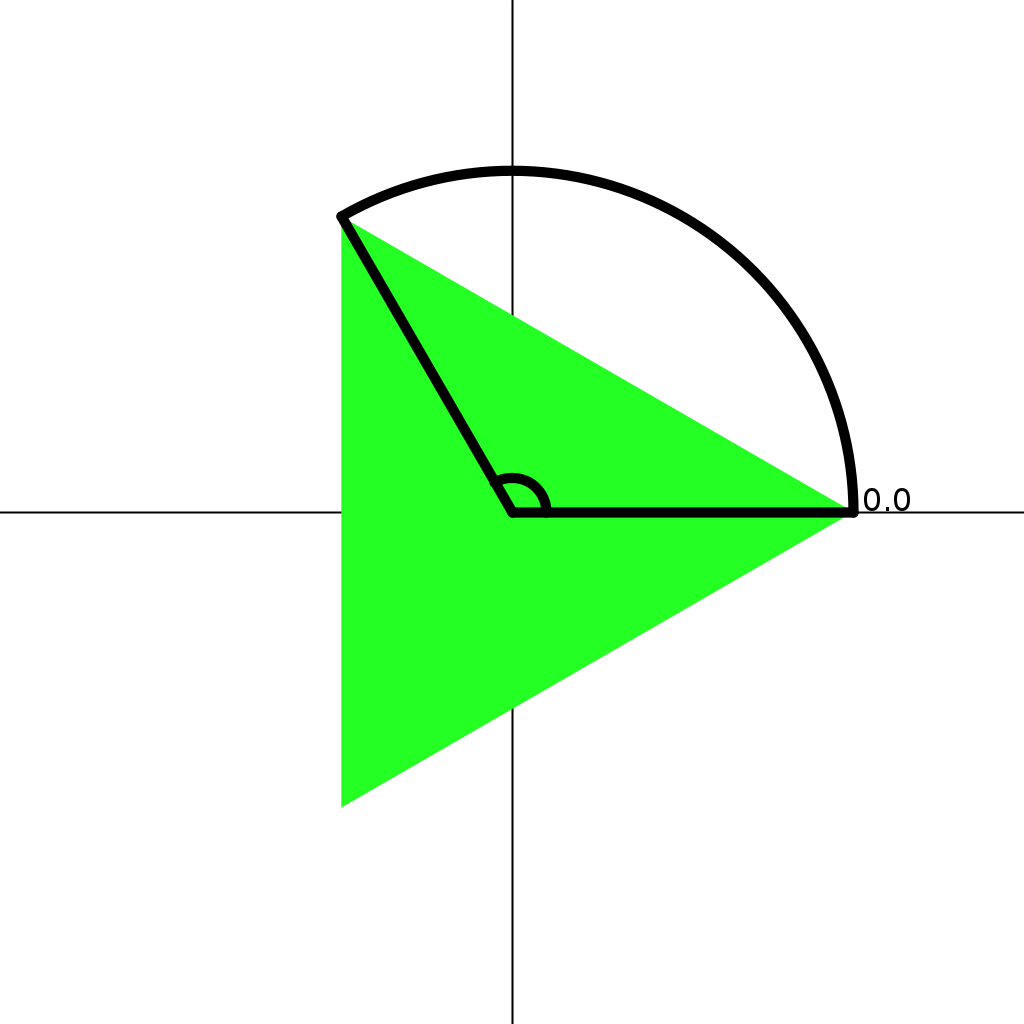
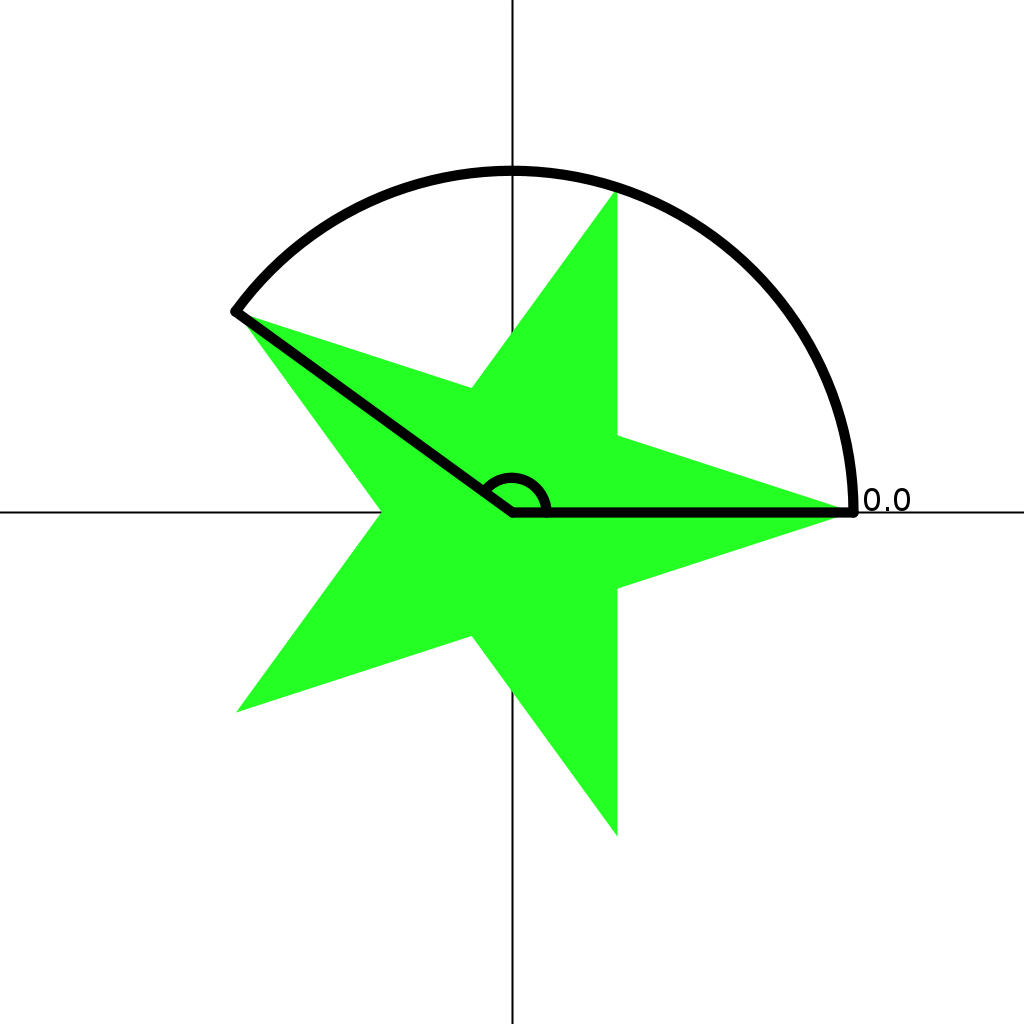
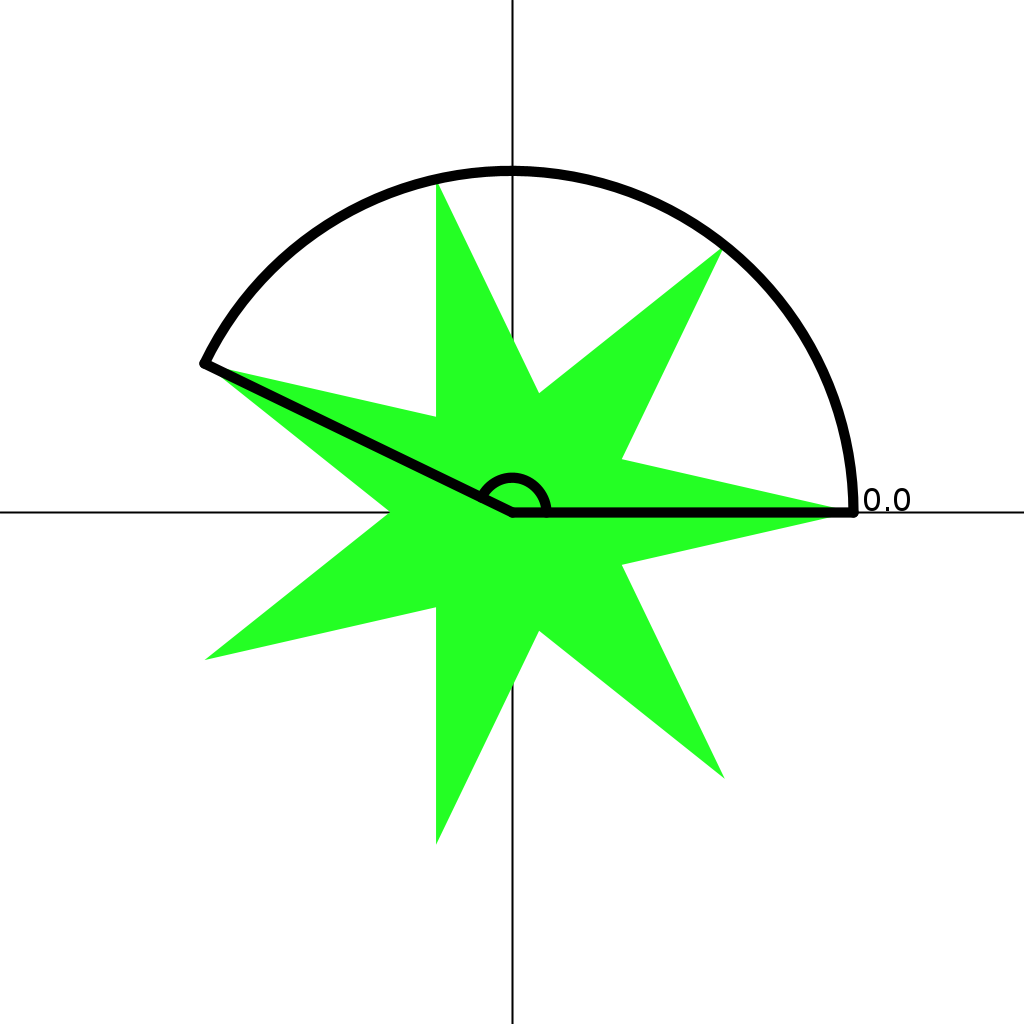
Look at the images below for 3, 5, and 7 pointed stars. Come up with a plan to fill odd pointed stars
3 Pointed Star (a.k.a. Equilateral Triangle)
5 Pointed Star
7 Pointed Star
Demo Video¶
In the video below, Prof Cosgrove discusses: - Definition for revolution: how many full circles the pen tip travelled while drawing a star (the process of drawing a star, see the second video). - How to test your code - What correct stars look like - How it is used in flags
How Many Revolutions?¶
How many complete revolutions will a 3 pointed star require? A 5 pointed star? A 7 pointed star? A 9 pointed star? …
Implement the method calculateRevolutionsForPoints(numPoints)
Note: Be sure to delete the throw new NotYetImplementedException(); line.
private static double calculateRevolutionsForPoints(int numPoints) {
// Delete the line below and implement this method
throw new NotYetImplementedException();
}
Inspect calculateTotalThetaInRadians¶
Revolutions might be the right unit to think about how many times around the circle you need to go for a particular pointed star. Math.cos(angleInRadians) and Math.sin(angleInRadians) are specified in radians. This method will convert from revolutions to radians for you.
Fill Odd Pointed Star¶
Note the provided lines in filledOddPointedStar(xCenter, yCenter, radius, numPoints, theta0InRadians). You can count on the fact that nPoints is odd and at least 3.
public static void filledOddPointedStar(double xCenter, double yCenter, double radius,
int numPoints, double theta0InRadians) {
if (numPoints % 2 == 0) {
throw new IllegalArgumentException();
}
if (numPoints < 3) {
throw new IllegalArgumentException();
}
//
// FIXME Your code goes here
//
}
Implement your clean, elegant solution to this problem. If you find yourself with if statements handling the different number of points separately you are on the wrong path and will NOT receive credit for this extension.
Testing¶
Star¶
Run Star.java as a Java Program.
You should see a spinning trinagle, and be prompted to continue. Then a smaller triangle in a different location, and another prompt. Then a 5 pointed star…
Note: See demo video above.
Singapore Flag¶
Inspect SingaporeFlag.java. Note that we take advantage of the fact that we can use the Flag of Indonesia (which in turn can use the Mother of All Flags, Norway).
Ask yourself:
How is the crescent created?
How are the stars placed?
Run SingaporeFlag.java as a Java Program.

Australian Flag Minus Union Jack¶
Inspect AustraliaFlagMinusUnionJack.java. Note the different number pointed stars.
Run AustraliaFlagMinusUnionJack.java as a Java Program.
