Extension 5.5: Net Present Value (2 points)

Authors

Background

In this assignment, we consider and reason about the [time value of money](https://en.wikipedia.org/wiki/Time_value_of_money).

This is based on the observations:

  • While we live in the present, we understand the value of $1 in terms of what it can buy today.

  • It’s difficult for us to think of what a dollar could buy 100 years ago or 100 years from now.

  • If we want to compare monetary values from several time periods, it is helpful to view them in the same time period.

The suggestion is therefore to reason about all currency in today’s dollars. This is called present value.

The ideas discussed here are widely used in economics, finance, and accounting.

Two Friends and your $1

Suppose you have $1 and two friends who offer to take your dollar under the following circumstances:

Friend One: This friend takes your $1 and gives you back $5 tomorrow.

Friend Two: This friend takes your $1 and gives you back $10 in fifty years.

Which friend is offering you the better deal?

If we consider only the number of dollars you receive from these two friends, then in 50 years you end up with either $5, or $10. It may therefore seem that Friend Two is offering you the better deal. However, we know that $10 fifty years from now is not worth $10 today.

How do we reason about the value of $10 in fifty years? We must first model how the value of money changes over time. We do this by choosing:

  • a time period during which the money’s value stays the same and at the end of which money grows instantaneously by some factor r. For this exercise, we choose a year’s time, so that money changes value annually.

  • a factor r, which is interchangeably called the discount rate, opportunity cost of capital, and rate of return. For this exercise, we choose 10% growth so that r=0.1.

We then use the time value of money to compute the following:

  • What would $1 be worth in fifty years if invested with some rate of return r? We model this computation by the function

\[futureValue(dollars, years, r) = dollars * (1.0 + r)^{years}\]

Thus, using r=.1, $1 is the same now as $117 dollars fifty years from now.

  • A “reverse” question is also interesting: How much would I have to set aside today so that it would be worth $1 in fifty years using the discount rate r? We model this computation by computing the reverse (running time backwards) of what we computed for the future:

\[presentValue(dollars, years, r) = \frac{dollars}{(1.0 + r)^{years}}\]

Thus, to have $1 fifty years from now, we would have to set aside 0.854 cents (less than one cent) now.

Friends Revisited

Returning to your two friends, let’s relate both friends’ offers in terms of present value, and compute your profit or loss (your net result). Recall we assume a discount rate of 10% (r=0.10) and we regard time annually.

Friend One

This friend takes your $1 and gives you back $5 tomorrow. Since value only changes value annually, $5 tomorrow is the same as $5 today.

\[presentValue($5, 0, 0.10) = \frac{$5}{(1.0 + 0.10)^0} = $5\]

Your net gain is the $5 you receive minus the $1 you gave away, so you net $4.

Friend Two

This friend takes your $1 and gives you back $10 in fifty years. $10 sounds better than $5, but adjusting the $10 in fifty years into it’s present value:

\[presentValue($10, 50, 0.10) = \frac{$10}{(1.0 + 0.10)^{50}} = $0.08\]

  • Your net gain is the 0.08 dollars you receive minus the $1 you gave away, so you net -0.92 dollars (you lose money on this deal).

Product Development Story

Consider the following example from Wikipedia, based on investing $100,000 to create a new product:

  • The product would cost you $100,000 to develop. That money would be gone forever.

  • Every year for the next 12 years, you would receive a $10,000 payout from sales of the product.

In summary, you give away $100,000 and you get $120,000 back. Is this a good deal? Let’s look at the returns in terms of Net Present Value (NPV). The table below shows:

Cash Flow: How much income or expense we have for the year. In year 0 we pay an investment, in all other years we receive a payout.

Present Value: Calculated by taking the cash flow for the year and converting it to its value in today’s dollars via the formula

Net Present Value: Calculated by taking the sum of this row’s present value and the present value of all previous years.

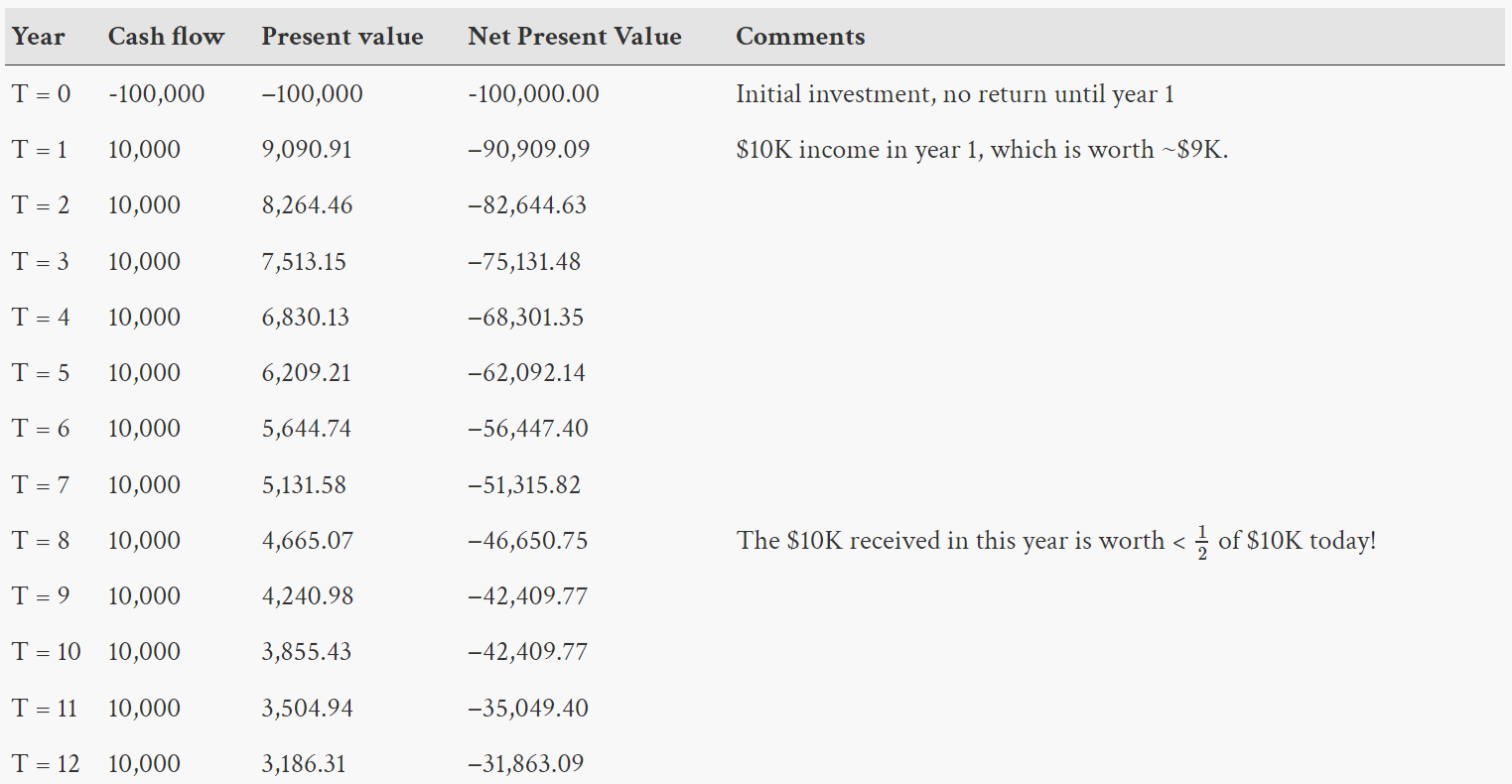
../_images/table.png

At the end of 12 years, we have $120,000 (The $10,000 per year for 12 years) but each year the $10,000 that we get has less buying power than it would have today (each year’s adjustment to a “present value”). If we sum those adjusted values, we have a total income of that is equivalent to $68,136.91 today for our expense of $100,000. Consequently, the NPV of the $100,000 investment is −31,863.09, which is a substantial loss. Because the NPV is negative, this is not an investment you should make.

Demo Video

Warning

The Product Development Story from Wikipedia has the unfortunate characteristic that investment * rate == payout. This can result in the surprising result that incorrect implementations of netPresentValue() will pass this case but fail all of the other test cases (which test netPresentValue() more rigorously).

Procedure

  • Find and open the NPV class found in the netpresentvalue package of the src folder in your repository. Using the information provided above, complete the methods.

  • Check your work by running the provided NPVTestSuite.java as a JUnit Test.

  • Run ProductDevelopmentStoryTable.java as a Java Application which should produce:

Year

Present Value

Net Present Value

T= 0

-100000.00

-100000.00

T= 1

9090.91

-90909.09

T= 2

8264.46

-82644.63

T= 3

7513.15

-75131.48

T= 4

6830.13

-68301.35

T= 5

6209.21

-62092.13

T= 6

5644.74

-56447.39

T= 7

5131.58

-51315.81

T= 8

4665.07

-46650.74

T= 9

4240.98

-42409.76

T=10

3855.43

-38554.33

T=11

3504.94

-35049.39

T=12

3186.31

-31863.08
Note: Your table may differ from wikipedia’s results by a cent.

https://en.wikipedia.org/wiki/Net_present_value#Example This appears to be due to wikipedia rounding each year to the nearest cent. Do not worry about this difference.

You have attempted of activities on this page