What is Recursion?

Recursion is when a method calls itself. See the example method below.

1public static void neverEnd() {
2  System.out.println("This is the method that never ends!");
3  neverEnd();
4}

This method will print out “This is the method that never ends!” and then call itself, which will print out the message again, and then call itself, and so on. This is called infinite recursion, which is a recursion that never ends. Of course, this particular method is not very useful.

exercise Check your Understanding

Why use Recursion?

Recursion is most useful when it is used to solve problems where the structure of the problem repeats. For example, what if you wanted to find out how much space a folder on your computers uses? You could add up the sizes of all the files in that folder, but folders can also contain subfolders. So you will have to repeat the procedure (method) for each subfolder. Each subfolder can also contain subfolders.

Recursion can also be used to create fractals. A simple example is Sierpinski’s triangle in which you subdivide a triangle into 4 new triangles as shown below. You can then do the some procedure with each new triangle except the center one.

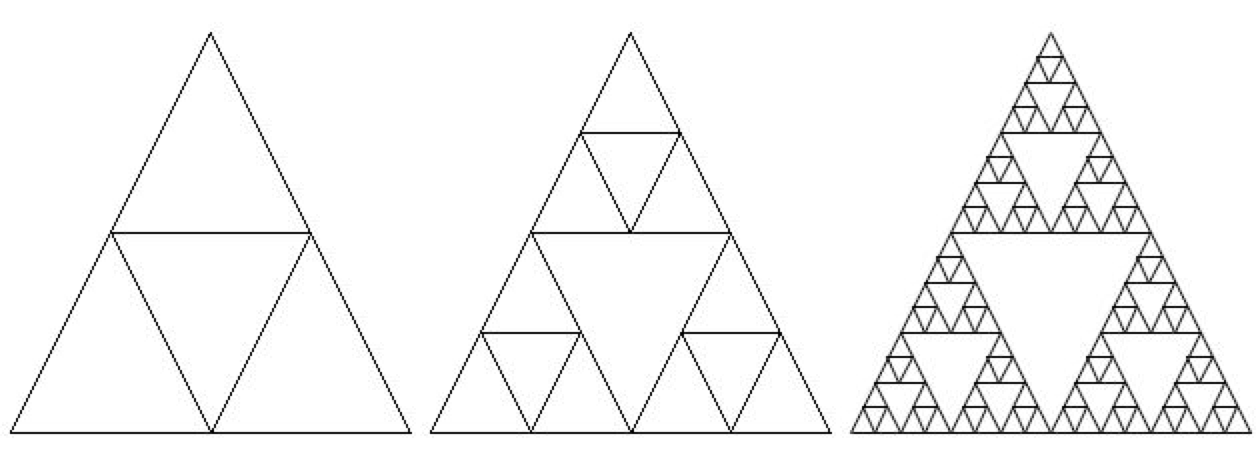
../_images/triangleSub.png

Figure 1: A sequence of Sierpinski’s triangles

Recursion can also be used to traverse String, array, and ArrayList objects, much like a loop. In fact, any recursive solution could be written with iteration (loops) instead.

Factorial Method

The following video is also on YouTube at https://youtu.be/V2S_8E_ubBY. It introduces the concept of recursion and tracing recursion with the factorial method.

See the method factorial below that calculates the factorial of a number. The factorial of a number is defined as 1 for 0 and n * factorial (n-1) for any other number.

1public static int factorial(int n) {
2    if (n == 0) {
3        return 1;
4    } else {
5        return n * factorial(n-1);
6        }
7}

exercise Check your understanding

coding exercise Coding Exercise

Run the E01FactorialTest program to test the factorial method. What’s the factorial of 6? Add another test to print out the factorial of 6. What’s the factorial of 1? Add another test to print out the factorial of 1.

Base Case

Every recursive method must have at least one base case which halts the recursion. This is usually an if statement that causes the recursion to stop by just giving an answer without needing a recursive method call. You could also think of it as the simplest case where you can give the answer right away. The factorial method has a way to stop the recursion (not call itself). It stops when n is equal to 0, since it just returns 1. This is the base case.

Note

The thing that stops a recursive method from calling itself is called the base case. A method can have more than one base case (way to stop the recursion).

exercise Check your understanding

Tracing Recursive Methods

In Java, the call stack keeps track of the methods that you have called since the main method executes. A stack is a way of organizing data that adds and removes items only from the top of the stack. An example is a stack of cups. You can grap a cup from the top of the stack or add more cups at the top of the stack.

../_images/cupStack.jpg

Figure 2: Stacks of cups

When you are executing one method (method a) and it calls another method (method b) the method call is placed on the call stack along with information about where it was called from, which tells the run-time where to return to when the current method finishes executing. When method b finishes executing the run-time pops the method b off of the call stack and returns execution to the next line to be executed in method a.

Consider the following class definition.

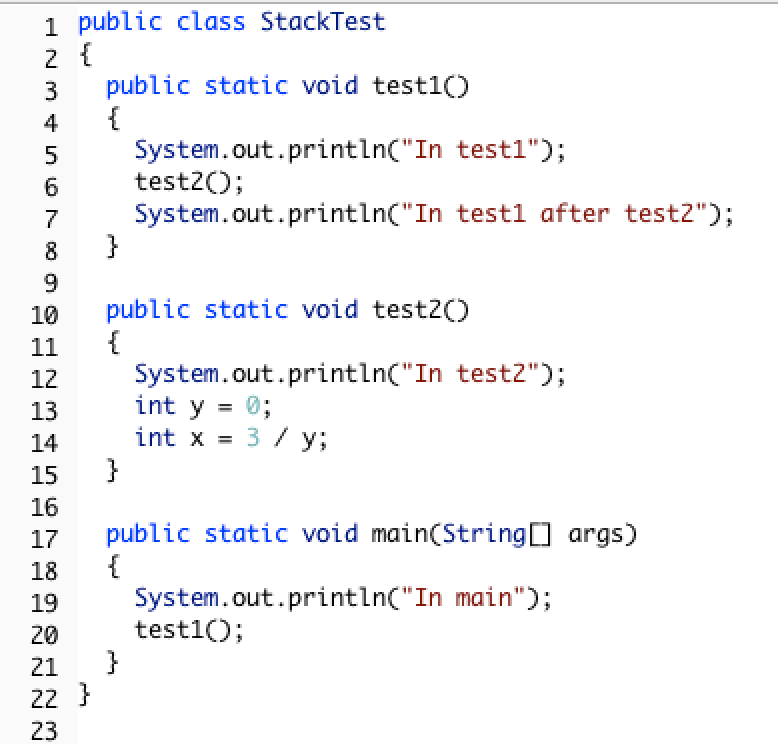
../_images/codeForCallStack.png

Figure 3: Code with a divide by zero in a method.

The code above will cause a run-time error of division by zero when it runs. The main method calls the method test1 (at line 20) which calls the method test2 (at line 6) which has the divide by zero error (line 14). This can be seen in the call stack shown below which shows the call stack from the top (most recent method) to the bottom (first method call).

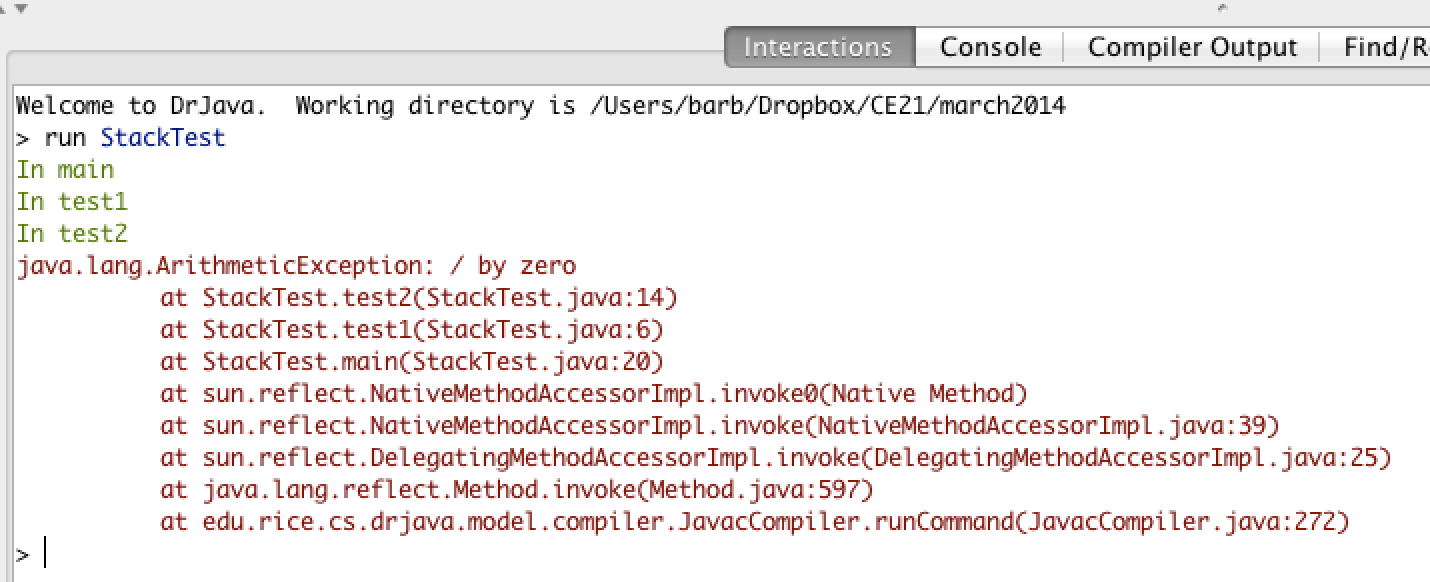
../_images/errorCallStack.png

Figure 4: A call stack in DrJava with a run-time error

When a method calls itself the new method call gets added to the top of the call stack. Execution of the current method pauses while the recursive call is being processed. Each recursive call on the stack has its own set of local variables, including the parameter variables. The parameter values progressively change in each recursive call until we reach the base case which stops the recursion.

coding exercise Tracing Exercise

Let’s trace the execution of the factorial method defined below.

1public static int factorial(int n) {
2  if (n == 0) {
3    return 1;
4  } else {
5    return n * factorial(n-1);
6      }
7}

What happens when we call factorial(0)? It will return 1 (line 4) since n is equal to 0. How about factorial(1)? It will return 1 * factorial(0). We already know that factorial(0) returns 1, but the computer won’t remember that. It will execute factorial(0) and return the result (1). So factorial(1) returns 1 * 1 which is 1.

How can you show what is happening in a recursive call? Here is one way to do it. The lines below show the call stack upside down (with the bottom of the stack, or the beginning at the top and the most recent call at the bottom) for a call to factorial(5). This is a handy way to trace a recursive method on the exam and you will do much better on recursive problems if you practice doing it this way.

1factorial(5) returns 5 * factorial(4)
2factorial(4) returns 4 * factorial(3)
3factorial(3) returns 3 * factorial(2)
4factorial(2) returns 2 * factorial(1)
5factorial(1) returns 1 * factorial(0)
6factorial(0) returns 1

Once factorial(0) executes and returns 1 that value can be substituted back into the previous method call, starting at the top of the stack (shown at the bottom here) and working our way back to the bottom of the stack (shown at the top here).

1factorial(5) returns 5 * factorial(4) = 5 * 24 = 120
2factorial(4) returns 4 * factorial(3) = 4 * 6 = 24
3factorial(3) returns 3 * factorial(2) = 2 so 3 * 2 = 6
4factorial(2) returns 2 * factorial(1) = 1 so 2 * 1 = 2
5factorial(1) returns 1 * factorial(0) = 1 so 1 * 1 = 1
6factorial(0) returns 1

So factorial(5) returns 120.

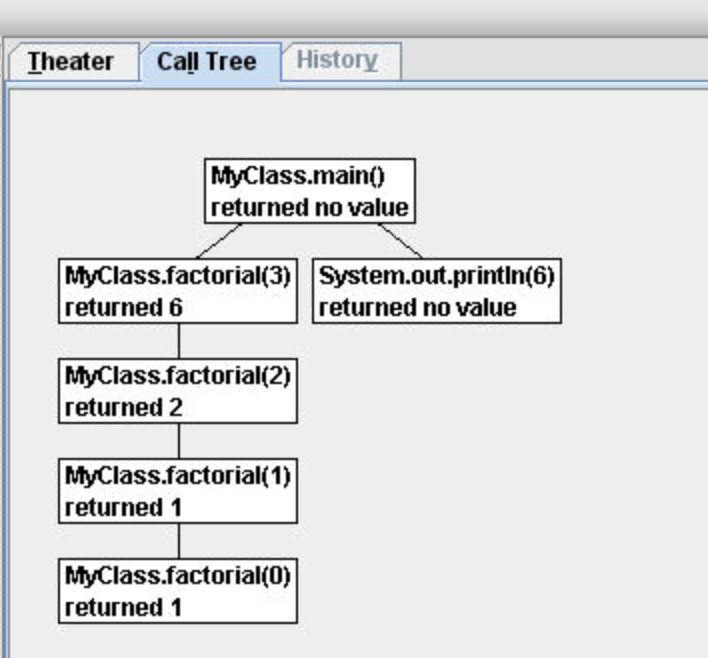
../_images/callTree.png

Figure 5: A call tree in Jeliot

exercise Check your understanding

coding exercise Tracing Exercise

Let’s trace the execution of the bunny ears method defined below.

1public static int bunnyEars(int bunnies) {
2   if (bunnies == 0) {
3              return 0;
4   } else if (bunnies == 1) {
5              return 2;
6   } else {
7              return 2 + bunnyEars(bunnies - 1);
8       }
9}

What happens when we call bunnyEars(0)? It will return 0 since n is equal to 0 (line 3). How about bunnyEars(1)? It will return 2 since n is equal to 1 (line 4). What about bunnyEars(5)?

1bunnyEars(5) returns 2 + bunnyEars(4)
2bunnyEars(4) returns 2 + bunnyEars(3)
3bunnyEars(3) returns 2 + bunnyEars(2)
4bunnyEars(2) returns 2 + bunnyEars(1)
5bunnyEars(1) returns 2

This approach shows the call stack from bottom to top. Once bunnyEars(1) executes and returns 2 that value can be substituted back into the previous method call, starting at the top and working our way back toward the bottom (or beginning) of the call stack.

1bunnyEars(5) returns 2 + bunnyEars(4) = 2 + 8 = 10
2bunnyEars(4) returns 2 + bunnyEars(3) = 2 + 6 = 8
3bunnyEars(3) returns 2 + bunnyEars(2) = 2 + 4 = 6
4bunnyEars(2) returns 2 + bunnyEars(1) = 2 + 2 = 4
5bunnyEars(1) returns 2

So bunnyEars(5) returns 10. You can step through this code using the Java Visualizer by clicking on this link: bunnyEars.

exercise Check your understanding

You can step through the code above using the Java Visualizer by clicking on the following link: Ex-11-3-4.

Tracing Challenge : Recursion

Trace through the following recursion problems.

Consider the following recursive method:

1public static int mystery(int n) {
2    if (n == 0) {
3        return 1;
4    } else {
5        return 3 * mystery (n - 1);
6        }
7}

The trace of this code for mystery(4) is shown below.

1mystery(4) returns 3 * mystery(3)
2mystery(3) returns 3 * mystery(2)
3mystery(2) returns 3 * mystery(1)
4mystery(1) returns 3 * mystery(0)
5mystery(0) returns A

Once mystery(0) returns 1 the value for each call to mystery can now be calculated and returned.

1mystery(4) returns 3 * mystery(3) = 3 * X = Y
2mystery(3) returns 3 * mystery(2) = 3 * 9 = 27
3mystery(2) returns 3 * mystery(1) = 3 * 3 = 9
4mystery(1) returns 3 * mystery(0) = 3 * 1 = 3
5mystery(0) returns 1

Consider the following recursive method:

 1public static int strMethod(String str) {
 2   if (str.length() == 1) {
 3             return 0;
 4   } else {
 5      if (str.substring(0,1).equals("e")) {
 6                     return 1 + strMethod(str.substring(1));
 7      } else {
 8                     return strMethod(str.substring(1));
 9              }
10   }
11}

1strMethod("every") returns 1 + strMethod("very")
2strMethod("very") returns strMethod("ery")
3strMethod("ery") returns 1 + strMethod("ry")
4strMethod("ry") returns strMethod("y")
5strMethod("y") returns B

Once strMethod(“y”) returns, the value from each recursive call on the stack can be calculated and returned.

1strMethod("every") returns 1 + strMethod("very") = Z
2strMethod("very") returns strMethod("ery") = Y
3strMethod("ery") returns 1 + strMethod("ry") = 1 + X
4strMethod("ry") returns strMethod("y") = 0
5strMethod("y") returns 0

Summary

You have attempted of activities on this page